Dispersion (from Lat. dispergere, to scatter), the act or process of separation and distribution. Apart from the technical use of the term, especially in optics (see below), the expression particularly applied to the settlements of Jews in foreign countries outside Palestine. These were either voluntary, for purposes of trade and commerce, or the results of conquest, such as the captivities of Assyria and Babylonia. The word diaspora (Gr. διασπορά) is also used of these scattered communities, but is usually confined to the dispersion among the Hellenic and Roman peoples, or to the body of Christian Jews outside Palestine (see Jews).
 |
| Fig. 1. |
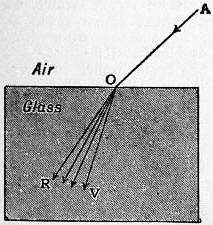
Dispersion, in Optics. When a beam of light which is not homogeneous in character, i.e. which does not consist of simple vibrations of a definite wave-length, undergoes refraction at the surface of any transparent medium, the different colours corresponding to the different wave-lengths become separated or dispersed. Thus, if a ray of white light AO (fig. 1) enters obliquely into the surface of a block of glass at O, it gives rise to the divergent system of rays ORV, varying continuously in colour from red to violet, the red ray OR being least refracted and the violet ray OV most so. The order of the successive colours in all colourless transparent media is red, orange, yellow, green, blue, indigo and violet. Dispersion is therefore due to the fact that rays of different colours possess different refrangibilities.
 |
| Fig. 2. |
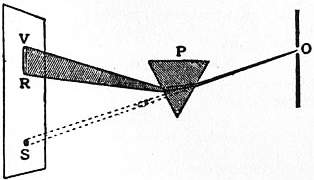
The simplest way of showing dispersion is to refract a narrow beam of sunlight through a prism of glass or prismatic vessel containing water or other clear liquid. As the light is twice refracted, the dispersion is increased, and the rays, after transmission through the prism, form a divergent system, which may be allowed to fall on a sheet of white paper, forming the well-known solar spectrum. This method was employed by Sir Isaac Newton, whose experiments constitute the earliest systematic investigation of the phenomenon. Let O (fig. 2) represent a small hole in the shutter of a darkened room, and OS a narrow beam of sunlight which is allowed to fall on a white screen so as to form an image of the sun at S. If now the prism P be interposed as in the figure, the whole beam is not only refracted upward, but also spread out into the spectrum RV, the horizontal breadth of the band of colours being the same as that of the original image S. In an experiment similar to that here represented, Newton made a small hole in the screen and another small hole in a second screen placed behind the first. By slightly turning the prism P, the position of the spectrum on the first screen could be shifted sufficiently to cause light of any desired colour to pass through. Some of this light also passed through the second hole, and thus he obtained a narrow beam of practically homogeneous light in a fixed direction (the line joining the apertures in the two screens). Operating on this beam with a second prism, he found that the homogeneous light was not dispersed, and also that it was more refracted the nearer the point from which it was taken approached to the violet end of the spectrum RV. This confirmed his previous conclusion that the rays increase in refrangibility from red to violet.
 |
| Fig. 3.—Method of Crossed Prisms. |
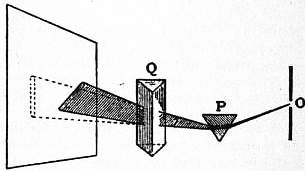
Newton also made use of the method of crossed prisms, which has been found of great use in studying dispersion. The prism P (fig. 3) refracts upwards, while the prism Q, which has its refracting edge perpendicular to that of P, refracts towards the right. The combined effect of the two is to produce a spectrum sloping up from left to right. The spectrum will be straight if the two prisms are similar in dispersive property, but if one of them is constructed of a material which possesses any peculiarity in this respect it will be revealed by the curvature of the spectrum.
The coloured borders seen in the images produced by simple lenses are due to dispersion. The explanation of the colours of the rainbow, which are also due to dispersion, was given by Newton, although it was known previously to be due to refraction in the drops of rain (see Rainbow).
According to the wave-theory of light, refraction (q.v.) is due to a change of velocity when light passes from one medium to another. The phenomenon of dispersion shows that in dispersive media the velocity is different for lights of different wave-lengths. In free space, light of all wave-lengths is propagated with the same velocity, as is shown by the fact that stars, when occulted by the moon or planets, preserve their white colour up to the last moment of disappearance, which would not be the case if one colour reached the eye later than another. The absence of colour changes in variable stars or in the appearance of new stars is further evidence of the same fact. All material media, however, are more or less dispersive. In air and other gases, at ordinary pressures, the dispersion is very small, because the refractivity is small. The dispersive powers of gases are, however, generally comparable with those of liquids and solids.
Dispersive Power.—In order to find the amount of dispersion caused by any given prism, the deviations produced by it on two rays of any definite pure colours may be measured. The angle of difference between these deviations is called the dispersion for those rays. For this purpose the C and F lines in the spark-spectrum of hydrogen, situated in the red and blue respectively, are usually employed. If δF and δC are the angular deviations of these rays, then δF − δC is called the mean dispersion of the prism. If the refracting angle of the prism is small, then the ratio of the dispersion to the mean deviation of the two rays is the dispersive power of the material of the prism. Instead of the mean deviation, ½ (δF + δC), it is more usual to take the deviation of some intermediate ray. The exact position of the selected ray does not matter much, but the yellow D line of sodium is the most convenient. If we denote its deviation by δD, then we may put
Dispersive power = (δF - δC)/δD (1).
This quantity may readily be expressed in terms of the refractive indices for the three colours, for if A is the angle of the prism (supposedly small)
δC = (μC − 1)A, δD = (μD − 1)A, δF = (μF − 1)A,
where μC, μD, μF are the respective indices of refraction. This gives at once
Dispersive power = (μF − μC)/(μD − 1) (2).
The second of these two expressions is generally given as the definition of dispersive power. It is more useful than (1), as the refractive indices may be measured with a prism of any convenient angle.
By studying the dispersion of colours in water, turpentine and crown glass Newton was led to suppose that dispersion is proportional to refraction. He concluded that there could be no refraction without dispersion, and hence that achromatism was impossible of attainment (see Aberration). This conclusion was proved to be erroneous when Chester M. Hall in 1733 constructed achromatic lenses. Glasses can now be made differing considerably both in refractivity and dispersive power.
Irrationality of Dispersion.—If we compare the spectrum produced by refraction in a glass prism with that of a diffraction grating, we find not only that the order of colours is reversed, but also that the same colours do not occupy corresponding lengths on the two spectra, the blue and violet being much more extended in the refraction spectrum. The refraction spectra for different media also differ amongst themselves. This shows that the connexion between the refrangibility of light and its wave-length does not obey any simple law, but depends on the nature of the refracting medium. This property is referred to as the “irrationality of dispersion.” In a diffraction spectrum the diffraction is proportional to the wave_length, and the spectrum is said to be “normal.” If the increase of the angle of refraction were proportional to the diminution of wave-length for a prism of any material, the resulting spectrum would also be normal. This, however, is not the case with ordinary refracting media, the refrangibility generally increasing more and more rapidly as the wave-length diminishes.
The irrationality of dispersion is well illustrated by C. Christiansen’s experiments on the dispersive properties of white powders. If the powder of a transparent substance is immersed in a liquid of the same refractive index, the mixture becomes transparent and a measurement of the refractive index of the liquid gives the refractivity of the powder. Christiansen found, in an investigation of this kind, that the refractivity of the liquid could only be got to match that of the powder for mono-chromatic light, and that, if white light were used, brilliant colour effects were obtained, which varied in a remarkable manner when small changes occurred in the refractive index of the liquid. These effects are due to the difference in dispersive power of the powder and the liquid. If the refractive index is, for instance, the same for both in the case of green light, and a source of white light is viewed through the mixture, the green component will be completely transmitted, while the other colours are more or less scattered by multiple reflections and refractions at the surfaces of the powdered substance. Very striking colour changes are observed, according to R. W. Wood, when white light is transmitted through a paste made of powdered quartz and a mixture of carbon bisulphide with benzol having the same refractive index as the quartz for yellow light. In this case small temperature changes alter the refractivity of the liquid without appreciably affecting the quartz. R. W. Wood has studied the iridescent colours seen when a precipitate of potassium silicofluoride is produced by adding silicofluoric acid to a solution of potassium chloride, and found that they are due to the same cause, the refractive index of the minute crystals precipitated being about the same as that of the solution, which latter can be varied by dilution.
Anomalous Dispersion.—In some media the usual order of the colours is changed. This curious phenomenon was noticed by W. H. Fox Talbot about 1840, but does not seem to have become generally known. In 1860 F. P. Leroux discovered that iodine vapour refracted the red rays more than the violet, the intermediate colours not being transmitted; and in 1870 Christiansen found that an alcoholic solution of fuchsine refracted the violet less than the red, the order of the successive colours being violet, red, orange, yellow; the green being absorbed and a dark interval occurring between the violet and red. A. Kundt found that similar effects occur with a large number of substances, in particular with all those which possess the property of “surface colour,” i.e., which strongly reflect light of a definite colour, as do many of the aniline dyes. Such bodies show strong absorption bands in those colours which they reflect, while of the transmitted light that which is of a slightly greater wave-length than the absorbed light has an abnormally great refrangibility, and that of a slightly shorter wave-length an abnormally small refrangibility. The name given to this phenomenon,—“anomalous dispersion”—is an unfortunate one, as it has been found to obey a regular law.
In studying the dispersion of the aniline dyes, a prism with a very small refracting angle is made of two glass plates slightly inclined to each other and enclosing a very thin wedge of the dye, which is either melted between the plates, or is in the form of a solution retained in position by surface-tension. Only very thin layers are sufficiently transparent to show the dispersion near or within an absorption band, and a large refracting angle is not required, the dispersion usually being very considerable. Another method, which has been used by R. W. Wood and C. E. Magnusson, is to introduce a thin film of the dye into one of the optical paths of a Michelson interferometer, and to determine the consequent displacement of the fringes. E. Mach and J. Arbes have used a method depending on total reflection (Drude’s Theory of Optics, p. 394).
 |
| Fig. 4.—Anomalous Dispersion of Sodium Vapour. |
 |
| Fig. 5. |
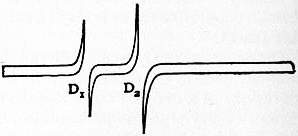
A very remarkable example of anomalous dispersion, which was first observed by A. Kundt, is that exhibited by the vapour of sodium. It has not been found practicable to make a prism of this vapour in the ordinary way by enclosing it in a glass vessel of the required shape, as sodium vapour attacks glass, quickly rendering it opaque. A. E. Becquerel, however, investigated the character of the dispersion by using prism-shaped flames strongly coloured with sodium. But the best way of exhibiting the effect is by making use of a remarkable property of sodium vapour discovered by R. W. Wood and employed for this purpose in a very ingenious manner. He found that when sodium is heated in a hard glass tube, the vapour which is formed is extraordinarily cohesive, only slowly spreading out in a cloud with well-defined borders, which can be rendered visible by placing the tube in front of a sodium flame, against which the cloud appears black. If a long glass tube with plane ends, and containing some pellets of sodium is heated in the middle by a row of burners, the cool ends remain practically vacuous and do not become obscured. The sodium vapour in the middle is very dense on the heated side, the density diminishing rapidly towards the upper part of the tube, so that, although not prismatic in form, it refracts like a prism owing to the variation in density. Thus if a horizontal slit is illuminated by an arc lamp, and the light-rendered parallel by a collimating lens—is transmitted through the sodium tube and focused on the vertical slit of a spectroscope, the effect of the sodium vapour is to produce its refraction spectrum vertically on the slit. The image of this seen through the glass prism of the spectroscope will appear as in fig. 4. The whole of the light, with the exception of a small part in the neighbourhood of the D lines, is practically undeviated, so that it illuminates only a very short piece of the slit and is spread out into the ordinary spectrum. But the light of slightly greater wave-length than the D lines, being refracted strongly downward by the sodium vapour, illuminates the bottom of the slit; while that of slightly shorter wave-length is refracted upward and illuminates the top of the slit. Fig. 4 represents the inverted image seen in the telescope. The light corresponding to the D lines and the space between them is absorbed, as evidenced by the dark interval. If the sodium is only gently heated, so as to produce a comparatively rarefied vapour, and a grating spectroscope employed, the spectrum obtained is like that shown in fig. 5, which was the effect noticed by Becquerel with the sodium flame. Here the light corresponding to the space between the D lines is transmitted, being strongly refracted upward near D1, and downward near D2.
The theory of anomalous dispersion has been applied in a very interesting way by W. H. Julius to explain the “flash spectrum” seen during a solar eclipse at the moment at which totality occurs. The conditions of this phenomenon have been imitated in the laboratory by Wood, and the corresponding effect obtained.
Theories of Dispersion.—The first attempt at a mathematical theory of dispersion was made by A. Cauchy and published in 1835. This was based on the assumption that the medium in which the light is propagated is discontinuous and molecular in character, the molecules being subject to a mutual attraction. Thus, if one molecule is disturbed from its mean position, it communicates the disturbance to its neighbours, and so a wave is propagated. The formula arrived at by Cauchy was
| n = A + | B | + | C | + .... |
| λ2 | λ4 |
n being the refractive index, λ the wave-length, and A, B, C, &c., constants depending on the material, which diminish so rapidly that only the first three as here written need be taken into account. If suitable values are chosen for these constants, the formula can be made to represent the dispersion of ordinary transparent media within the visible spectrum very well, but when extended to the infra-red region it often departs considerably from the truth, and it fails altogether in cases of anomalous dispersion. There are also grave theoretical objections to Cauchy’s formula.
The modern theory of dispersion, the foundation of which was laid by W. Sellmeier, is based upon the assumption that an interaction takes place between ether and matter. Sellmeier adopted the elastic-solid theory of the ether, and imagined the molecules to be attached to the ether surrounding them, but free to vibrate about their mean positions within a limited range. Thus the ether within the dispersive medium is loaded with molecules which are forced to perform oscillations of the same period as that of the transmitted wave. It can be shown mathematically that the velocity of propagation will be greatly increased if the frequency of the light-wave is slightly greater, and greatly diminished if it is slightly less than the natural frequency of the molecules; also that these effects become less and less marked as the difference in the two frequencies increases. This is exactly in accordance with the observed facts in the case of substances showing anomalous dispersion. Sellmeier’s theory did not take account of absorption, and cannot be applied to calculate the dispersion within a broad absorption band. H. von Helmholtz, working on a similar hypothesis, but with a frictional term introduced into his equations, obtained formulae which are applicable to cases of absorption. A modified form of Helmholtz’s equation, due to E. Ketteler and known as the Ketteler-Helmholtz formula, has been much used in calculating dispersion, and expresses the facts with remarkable accuracy. P. Drude has obtained a similar formula based on the electromagnetic theory, thus placing the theory of dispersion on a much more satisfactory basis. The fundamental assumption is that the medium contains positively and negatively charged ions or electrons which are acted on by the periodic electric forces which occur in wave propagation on Maxwell’s theory. The equations finally arrived at are
| n²(1 − κ²) = 1 + Σ | Dλ²(λ² − λm²) | , |
| (λ² − λm²)² + g²λ² |
| 2n²κ² = Σ | Dgλ³ | , |
| (λ² − λm²)² + g²λ² |
where λ is the wave-length in free ether of light whose refractive index is n, and λm the wave-length of light of the same period as the electron, κ is a coefficient of absorption, and D and g are constants. The sign of summation Σ is used in cases where there are several absorption bands, and consequently several similar terms on the right-hand side, each with a different value of λm. This would occur if there were several kinds of ions, each with its own natural period.
In a region where there is no absorption, we have κ = 0 and therefore g = 0, and we have only one equation, namely,
| n² = 1 + Σ | Dλ² | , |
| (λ² − λm²) |
which is identical with Sellmeier’s result. As λm, is a wave-length corresponding to an absorption band, this formula can be used to find values of λm which satisfy the observed values of n within the region of transparency, and so to determine where the absorption bands are situated. In this way the existence of bands in the infrared part of the spectrum has been predicted in the case of quartz and detected by experiments on the selective reflection of the material.
References.—For the theory of dispersion see P. Drude, Theory of Optics (Eng. trans.); R. W. Wood, Physical Optics; and A. Schuster, Theory of Optics. For descriptive accounts, see Wood’s Physical Optics, T. Preston’s Theory of Light, E. Edser’s Light. The last work contains an elementary treatment of Sellmeier’s theory.


