Cycloid (from Gr. κύκλος, circle, and εἶδος, form), in geometry, the curve traced out by a point carried on a circle which rolls along a straight line. The name cycloid is now restricted to the curve described when the tracing-point is on the circumference of the circle; if the point is either within or without the circle the curves are generally termed trochoids, but they are also known as the prolate and curtate cycloids respectively. The cycloid is the simplest member of the class of curves known as roulettes.
No mention of the cycloid has been found in writings prior to the 15th century. Francis Schooten (Commentary on Descartes) assigns the invention of the curve to René Descartes and the first publication on this subject after Descartes to Marin Mersenne. Evangelista Torricelli, in the first regular dissertation on the cycloid (De dimensione cycloidis, an appendix to his De dimensione parabolae, 1644), states that his friend and tutor Galileo discovered the curve about 1599. John Wallis discussed both the history and properties of the curve in a tract De cycloide published at Oxford in 1659. He there shows that the cycloid was investigated by Carolus Bovillus about 1500, and by Cardinal Cusanus (Nicolaus de Cusa) as early as 1451. Honoré Fabri (Synopsis geometrica, 1669) treated of the curve and enumerated many theorems concerning it. Many other mathematicians have written on the cycloid—Blaise Pascal, W. G. Leibnitz, the Bernoullis, Roger Cotes and others—and so assiduously was it studied that it was sometimes named the “Helen of Geometers.” The determination of the area was the subject of many investigations and much controversy. Galileo attempted the evaluation by weighing the curve against the generating circle; this rough method gave only an approximate value, viz., a little less than thrice the generating circle. Torricelli, by employing the “method of indivisibles,” deduced that the area was exactly three times that of the generating circle; this result had been previously established in 1640 in France by G. P. de Roberval, but his investigation was unknown in Italy. Blaise Pascal determined the area of the section made by any line parallel to the base and the volumes and centres of gravity of the solids generated by revolving the curve about its axis and base. Before publishing his results he proposed these problems for public competition in 1658 under the assumed name of Amos Dettonville. John Wallis in England, and A. la Louère in France, accepted the challenge, but the former could only submit incorrect solutions, while the latter failed completely. Having established his priority, Pascal published his investigations, which occasioned a great sensation among his contemporaries, and Wallis was enabled to correct his methods. Sir Christopher Wren, the famous architect, determined the length of the arc and its centre of gravity, and Pierre Fermat deduced the surface of the spindle generated by its revolution. A famous period in the history of the cycloid is marked by a bitter controversy which sprang up between Descartes and Roberval. The evaluation of the area of the curve had made Roberval famous in France, but Descartes considered that the value of his investigation had been grossly exaggerated; he declared the problem to be of an elementary nature and submitted a short and simple solution. At the same time he challenged Roberval and Fermat to construct the tangent; Roberval failed but Fermat succeeded. This problem was solved independently by Vicenzo Viviani in Italy. The cartesian equation was first given by Wilhelm Gottfried Leibnitz (Acta eruditorum, 1686) in the form y = (2x − x²)½ + ∫(2x − x²)½dx. Among other early writers on the cycloid were Phillippe de Lahire (1640-1718) and François Nicole (1683-1758).
The mechanical properties of the cycloid were investigated by Christiaan Huygens, who proved the curve to be tautochronous. His enquiries into evolutes enabled him to prove that the evolute of a cycloid was an equal cycloid, and by utilizing this property he constructed the isochronal pendulum generally known as the cycloidal pendulum. In 1697 John Bernoulli proposed the famous problem of the brachistochrone (see Mechanics), and it was proved by Leibnitz, Newton and several others that the cycloid was the required curve.
 |
| Fig. 1. |
 |
| Fig. 2. |
 |
| Fig. 3. |
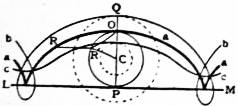
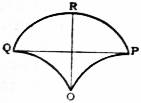
The method by which the cycloid is generated shows that it consists of an infinite number of cusps placed along the fixed line and separated by a constant distance equal to the circumference of the rolling circle. The name cycloid is usually restricted to the portion between two consecutive cusps (fig. 1, curve a); the fixed line LM is termed the base, and the line PQ which divides the curve symmetrically is the axis. The co-ordinates of any point R on the cycloid are expressible in the form x = a(θ + sin θ); y = a(1 − cos θ), where the co-ordinate axes are the tangent at the vertex O and the axis of the curve, a is the radius of the generating circle, and θ the angle R′CO, where RR′ is parallel to LM and C is the centre of the circle in its symmetric position. Eliminating θ between these two relations the equation is obtained in the form x = (2ay − y²)½ + a vers-¹ y/a. The clumsiness of the relation renders it practically useless, and the two separate relations in terms of a single parameter θ suffice for the deduction of most of the properties of the curve. The length of any arc may be determined by geometrical considerations or by the methods of the integral calculus. When measured from the vertex the results may be expressed in the forms s = 4a sin ½θ and s = √(8ay); the total length of the curve is 8a. The intrinsic equation is s = 4a sin ψ, and the equation to the evolute is s = 4a cos ψ, which proves the evolute to be a similar cycloid placed as in fig. 2, in which the curve QOP is the evolute and QPR the original cycloid. The radius of curvature at any point is readily deduced from the intrinsic equation and has the value ρ = 4 cos ½θ, and is equal to twice the normal which is 2a cos ½θ.
The trochoids were studied by Torricelli and F. van Schooten, and more completely by John Wallis, who showed that they possessed properties similar to those of the common cycloid. The cartesian equation in terms similar to those used above is x = aθ + b sin θ; y = a − b cos θ, where a is the radius of the generating circle and b the distance of the carried point from the centre of the circle. If the point is without the circle, i.e. if a < b, then the curve exhibits a succession of nodes or loops (fig. 1, curve b); if within the circle, i.e. if a > b, the curve has the form shown in fig. 1, curve c.
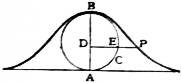
The companion to the cycloid is a curve so named on account of its similarity of construction, form and equation to the common cycloid. It is generated as follows: Let ABC be a circle having AB for a diameter. Draw any line DE perpendicular to AB and meeting the circle in E, and take a point P on DE such that the line DP = arc BE; then the locus of P is the companion to the cycloid. The curve is shown in fig. 3. The cartesian equation, referred to the fixed diameter and the tangent at B as axes may be expressed in the forms x = aθ, y = a(1 − cos θ) and y − a = a sin (x/a − ½π); the latter form shows that the locus is the harmonic curve.
For epi- and hypo-cycloids and epi- and hypo-trochoids see Epicycloid.
References.—Geometrical constructions relating to the curves above described are to be found in T. H. Eagles, Constructive Geometry of Plane Curves. For the mechanical and analytical investigation, reference may be made to articles Mechanics and Infinitesimal Calculus. A historical bibliography of these curves is given in Brocard, Notes de bibliographie des courbes géométriques (1897). See also Moritz Cantor, Geschichte der Mathematik (1894-1901).


